ТЕПЛОПРОВОДНОСТЬ В СРЕДАХ С ЦИЛИНДРИЧЕСКОЙ СИММЕТРИЕЙ

 

Рассмотрим задачу об остывании бесконечно длинного цилиндра радиуса R. Начальная температура цилиндра .  В момент  t = 0  он помещается в среду с температурой  и с бесконечной теплоемкостью. Следовательно, в процессе охлаждения температура поверхности не меняется и остается равной . Требуется найти пространственно- временнόе распределение температуры  внутри цилиндра при .  Знание его необходимо, например, для прогнозирования процесса закалки стали.

Запишем уравнение теплопроводности в цилиндрической системе координат, предполагая все теплофизические параметры постоянными:

                

Так как цилиндр бесконечно длинный, то поле температур не зависит от координаты  z . Вместо (4.105) имеем уравнение

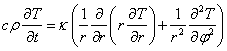                                  (4.105)

Начальные и  граничные условия имеют вид

                                                                     (4.106)

                                                                     (4.107)

Кроме этих условий, на функцию  следует наложить требование однозначности

                                                 (4.108)

Перейдем к безразмерным переменным

Задача (4.105) - (4.108) примет вид

       ,         

                                                     

                                                                     

                                                

Решение временной задачи  - ) в соответствии с теорией  метода разделения переменных  может быть представлено в виде

                    

где  - решение задачи Штурма – Лиувилля

                  

или                                                      (4.109)

                               ,                                         (4.110)

                                                     (4.111)

К ней также можно применить метод разделения переменных, представив  в виде

                                                        (4.112)

Подставим (4.112) в (4.110) и разделим переменные:

                       

                    

Первые три слагаемые зависят только от  , четвёртое – только от . Сумма их равна нулю только если 

                       

                              

Решение последнего уравнения имеет вид

        

Для удовлетворения условия однозначности (4.111) необходимо, чтобы

                         

Положим начальную фазу  равной нулю,  тогда

,                                (4.113)

Для   получаем уравнение

                                           (4.114)

Каждому значению m соответствует совокупность собственных функций и собственных значений, которые поэтому нумеруются двумя индексами, и . Индекс  m  характеризует симметрию вращения вокруг оси z, а индекс  n  - влияние радиального размера цилиндра.

Общее решение  запишется теперь в виде

            (4.115)

Уравнение  (4.114) с помощью замены переменной  можно записать в  эквивалентных формах

                                       

или                                             

Таким образом, мы приходим к необходимости изучить уравнение  или    и  свойства его решений. Оно известно с 1700 года и называется уравнением Бесселя в честь немецкого математика и астронома   Фридриха Бесселя, впервые систематически его изучившего в начале ХIХ века. Решения уравнений  , не равные тождественно нулю, называются цилиндрическими функциями.