КЛАСИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ

                                  

Из изложенного в главе 1 следует, что классические поля описываются дифференциальными уравнениями в частных производных, которые, в общем случае, содержат производные от искомой функции по времени и пространственным координатам, до второго порядка включительно, и саму искомую функцию. Причем как производные, так и искомая функция входят в уравнения линейно. Такие уравнения называются линейными уравнениями в частных производных. В общем виде они записываются следующим образом:

 (2.1)

где  , и  т.д. Коэффициенты   линейного уравнения могут явно зависеть от координат и времени, но не от искомой функции u.  Если они зависят от u, то уравнение (2.1) называется квазилинейным. Его можно записать в более компактной  форме

                                     (2.2)

- компоненты четырехмерного вектора . Уравнения (2.1) и (2.2) могут быть упрощены с помощью преобразования к новым переменным

                  

Рассмотрим сначала наиболее простой случай уравнения двух переменных

       (2.3)

Преобразование переменных в этом случае имеет вид

                                                     (2.4)

Искомая функция  u  зависит от   и  , . Для производных получаем

                  

                  

  

 

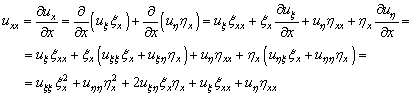
Аналогично

     

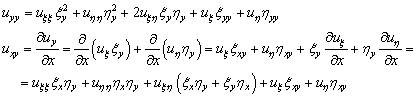
После подстановки в (2.4) и приведения подобных членов  получаем

           (2.5)

где        

      

        

        

      

Выберем      такой, чтобы коэффициент при  равнялся нулю. Для этого функция  должна удовлетворять уравнению

                                         (2.6)

Используем  лемму, доказанную, например, в учебнике А.Н.Тихонова и А.А.Самарского: функция  удовлетворяет уравнению (2.6), если  представляет собой первый интеграл обыкновенного дифференциального уравнения

                                            (2.7)

Уравнение (2.7) называется  характеристическим для уравнения (2.1), а его интегралы - характеристиками. Таким образом, общий интеграл уравнения (2.7) обращает в нуль коэффициент при . Если существует еще один, независимый, интеграл уравнения (2.7), то с его помощью можно обратить в нуль коэффициент при . Уравнение (2.7) можно преобразовать к виду

                                 

откуда получаем два уравнения характеристик

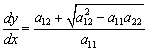                                                     (2.8)

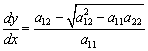                                                     (2.9)   

Знак подкоренного выражения в (2.8), (2.9) определяет тип уравнения  (2.1) в точке  .

         Если  , (2.1)              называется  уравнением

                                                                   гиперболического типа.

         Если  , (2.1) называется  уравнением  (2.10)

                                                       параболического типа       

         Если  , (2.1) называется  уравнением

                                                       эллиптического типа

 Так как , , являются в общем случае функциями координат, то в разных точках области определения уравнение (2.1) может принадлежать к разным типам.

Условия (2.10) задают каноническую форму соответствующего уравнения.