ОБОЩЁННЫЕ ФУНКЦИИ
До сих пор идут
дискуссии о том, является ли математика естественной наукой или нет? Другими
словами, имеют ли изучаемые ею объекты отношение к материальному миру, являются
ли они его порождением, так называемой объективной реальностью, или же они суть
порождение только человеческого мышления? Как бы то ни было, всегда
оказывалось, что все авангардные изобретения математиков находят со временем
применение при решении практических задач.
И, в свою очередь, практические потребности заставляют тщательнее
изучать некоторые давно известные
математические объекты. Так произошло и с понятием функции.
Понятие функции
- одно из основных в математике. Общее определение следующее: функцией
одного действительного переменного называется отображение подмножества А из множества R действительных
чисел в подмножество В из
R. А - область определения, В -
множество значений функции. Символически функция обозначается y = f(x). Наиболее
удобный способ задания функции - аналитико -
графический. При этом способе задается математическое соотношение между
аргументом х и значением функции у, например, ![]() ,
изображаемое графически (рис. 1д).
,
изображаемое графически (рис. 1д).

Рис 1д. График "хорошей" функции
Такое
представление функции позволяет наглядно описать ее свойства. Первоначально
математики интересовались только "хорошими" функциями, свойства
которых достаточны для описания реальных зависимостей между физическими
величинами. Эти реальные зависимости характеризовались плавностью изменения,
отсутствием скачков, ограниченностью определенными пределами. Поэтому "хорошие" математические
функции оказались носителями следующих свойств.
1. Функция f(x) является
непрерывной в любой точке ![]() ,
принадлежащей ее области определения D. Функция непрерывна в точке
,
принадлежащей ее области определения D. Функция непрерывна в точке ![]() тогда и только тогда, когда существует предел
тогда и только тогда, когда существует предел
![]()
Предел же существует тогда и только
тогда, когда для произвольной числовой
последовательности ![]() ,
для которой
,
для которой ![]() ,
имеют место соотношения
,
имеют место соотношения
![]()
![]()
2. Функция f(x) является дифференцируемой в точке x0, то есть
существует предел
![]()
3. Функция f(x) является
интегрируемой в D.
4. Функция f(x) может быть
разложена в интеграл Фурье. Для этого интервал ![]() должен допускать разбиение на конечное число интервалов монотонности и
непрерывности, а в точках разрыва должны существовать пределы справа и слева.
должен допускать разбиение на конечное число интервалов монотонности и
непрерывности, а в точках разрыва должны существовать пределы справа и слева.
Но по мере
развития техники для описания реальных процессов приходилось вводить в обиход
функции, которые нельзя было отнести к "хорошим". Например,
О.Хэвисайд в теоретическом анализе электрических цепей
широко использовал ступенчатую функцию, ныне называемую функцией Хэвисайда,
![]() (Д1.1)
(Д1.1)

Рис. 2д Ступенчатая
функция Хэвисайда
Она описывала
скачок тока или напряжения на входе электрической цепи. Интерес представлял
отклик системы, то есть сигнал на выходе. Импульс конечной длительности ![]() задается разностью функций Хэвисайда
задается разностью функций Хэвисайда ![]() .
Другим примером использования Функции
Хэвисайда является представление физических параметров неоднородных сред.
Например, плотность двухслойной среды
может быть записана в виде
.
Другим примером использования Функции
Хэвисайда является представление физических параметров неоднородных сред.
Например, плотность двухслойной среды
может быть записана в виде
![]()
Функция Хэвисайда, как легко видеть, не
имеет определенного предела в точке ![]() ,
поэтому она не дифференцируема в этой точке.
,
поэтому она не дифференцируема в этой точке.
Еще более
необычную функцию ввел в физику П.Дирак. Создавая релятивистскую квантовую
теорию, он столкнулся с проблемой нормировки волновой функции свободного
электрона. В волновой механике Шредингера условие нормировки атомной волновой функции записывается в виде
![]() (Д1.2)
(Д1.2)
Нормировка на 1
возможна потому, что атомные волновые функции удовлетворяют так
называемым естественным условиям, в то числе и условию ограниченности на
бесконечности,
![]() при
при ![]()
Волновая функция
свободного электрона - это
плоская волна
![]()
для которой ![]() ,
поэтому
,
поэтому
![]() (Д1.3)
(Д1.3)
В то же время
![]() (Д1.4)
(Д1.4)
Чтобы отразить в единой формуле
соотношения (Д1.3)
и (Д1.4), наподобие (Д1.2), Дирак
ввел специальную функцию ![]() ,
которую впоследствии стали называть
,
которую впоследствии стали называть ![]() -
функцией Дирака, определяемую соотношениями
-
функцией Дирака, определяемую соотношениями
![]() (Д1.5')
(Д1.5')
![]() (Д1.5'')
(Д1.5'')
Условие
нормировки запишется в виде
![]() (Д1.6)
(Д1.6)
С введенными
таким образом "физическими" функциями
надо было выполнять те же математические операции, что и с
"хорошими" функциями. Хотя физики выполняли их без особых угрызений
совести, возможность этого была не очевидна для математиков. Поэтому ими было
введено понятие обобщенных функций, к которым принадлежат ![]() и
и ![]() .
.
Обобщенная
функция определяется посредством предельного перехода по некоторому параметру
"хорошей" функции, передающей основные черты обобщенной. Наглядно эту
хорошую функцию можно получить "размазыванием" обобщенной функции по
некоторому интервалу. Например, функция Хэвисайда моделируется функцией
![]() (Д1.7)
(Д1.7)

В пределе получаем ![]() .
Посредством этого соотношения определяются операции над
.
Посредством этого соотношения определяются операции над
![]() .
В частности,
.
В частности,
![]()

Максимальное
значение функции ![]() достигается при x = 0 и равно
достигается при x = 0 и равно ![]() . Полуширина
ее на полувысоте получается из соотношения
. Полуширина
ее на полувысоте получается из соотношения ![]() и равна
и равна ![]() .
Таким образом,
.
Таким образом, ![]() ,
,
![]() ,
при этом
,
при этом
![]()
Следовательно, можно отождествить
![]() (Д1.9)
(Д1.9)
Математически строго доказано, что
представление (Д1.9) ![]() -
функции - не единственное. Существует много способов ее "размазывания",
то есть задания последовательностей
-
функции - не единственное. Существует много способов ее "размазывания",
то есть задания последовательностей ![]() .
Например,
.
Например,
![]() (Д1.9')
(Д1.9')
![]() (Д1.9'')
(Д1.9'')
![]() (Д1.9''')
(Д1.9''')
Из определения
(Д1.9) следуют свойства ![]() -
функции:
-
функции:
1. ![]()
2. ![]()
3. ![]()

4.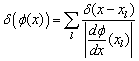 ,
где
,
где ![]() - нули
функции
- нули
функции ![]() ,
,
![]() .
.
Свойство 4.
становится очевидным, если в окрестности каждого нуля функции ![]() разложить ее в ряд Тейлора,
разложить ее в ряд Тейлора,
![]()
и воспользоваться свойством 2. (см. рис.)
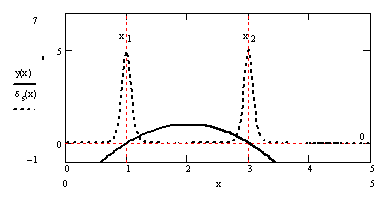 Рис. 2. Интегрирование с помощью
δ - функции
Рис. 2. Интегрирование с помощью
δ - функции
5. Фурье-преобразование ![]() - функции
имеет вид
- функции
имеет вид
![]()
![]()
6. Многомерные
![]() - функции определяются соотношениями:
- функции определяются соотношениями:
![]() в декартовой системе координат,
в декартовой системе координат,
![]() в полярной системе координат,
в полярной системе координат,
![]() в
сферической системе координат.
в
сферической системе координат.
Свойства 2. - 6. ![]() - функции широко используются при решении
задач математической физики.
- функции широко используются при решении
задач математической физики.