4.2.2        ЗАДАЧА КОШИ НА ПРЯМОЙ

 

Пусть задано начальное распределение температуры

                                           

Функцию  будем считать “хорошей”, так что все последующие математические операции законны. Требуется найти  температуру  при , то есть решить уравнение

                                                                      

Функция Грина задачи (4.322) удовлетворяет уравнению

                                                                     

и начальному условию                          

Для нахождения функции Грина совершим преобразование Фурье по x: умножим уравнение и начальное условие на  и проинтегрируем по x от  до .

                     

    

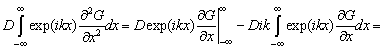
При интегрировании по частям было учтено, что  и  при .

                

Для фурье-образа  получаем уравнение первого порядка

                                                                    

Из  получаем начальное условие

                  

                                                           

Решение уравнения тривиально,

                              

Постоянную  находим из

                              

Таким образом,        

Выполняя обратное преобразование Фурье, приходим к искомой функции Грина

  

 

 

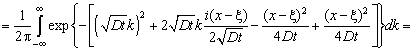
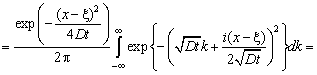
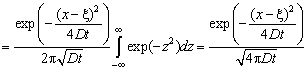            (4.322)

Частный случай 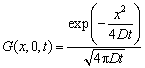                              (4.323)

называется фундаментальным решением уравнения теплопроводности. Таким образом, решение задачи (4.322) имеет вид

                          (4.324)