УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА.

 

1. Пусть требуется найти в области  D, ограниченной поверхностью S, при  решение однородной краевой задачи

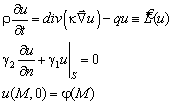                                              (4.306)

Если в D известно решение  задачи

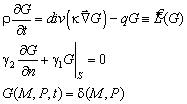                                                       (4.307)

где   -  - функция Дирака с особенностью в точке P, то

                                            (4.308)

В том, что (4.308) удовлетворяет задаче (4.306), легко убедиться прямой подстановкой.

            

                        

               

   

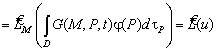
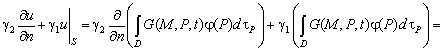
Таким образом, справедливость (4.308) установлена. Тем самым усилия переносятся на построение решения задачи (4.307), которое называется функцией Грина задачи (4.306).

2.Методом функций Грина может быть найдено и решение   неоднородной краевой задачи

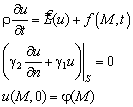                                 (4.309)

Для этого произведем редукцию задачи (4.309):

                     

           

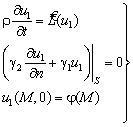
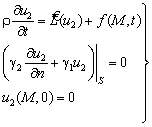
Решение задачи  построено в предыдущем пункте (формула (4.308)). Решение  будем искать в виде

                                                     (4.311)

При этом начальные условия удовлетворяются автоматически. Подставим (4.311) в .

                  

                  

                  

 удовлетворит , если  w  будет решением краевой задачи

                              

                              

                              

Последнее соотношение есть начальное условие для функции , записанное в момент . Согласно п.1

                  

Тогда                      (4.312)

Таким образом, решение неоднородной задачи (4.309) имеет вид

   (4.313)

3. Решение задачи Коши в безграничном пространстве

                    ,                          (4.314)           

также может быть выражено через функцию Грина , являющуюся решением задачи

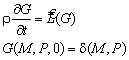                                                          (4.315)

При этом 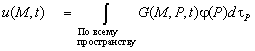              (4.316)

4. Решение неоднородной задачи Коши

                              

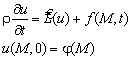
строится аналогично п.2,

      

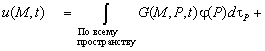
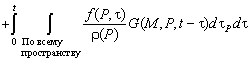                           (4.317)

Для ограниченных областей функция Грина может быть найдена методом разделения переменных. Фактически это и было сделано в п.4.1.2 при изложении общей теории метода разделения переменных (формулы (4.31) и (4.32) фактически совпадают с (4.313). Функция Грина краевой задачи для параболического уравнения выражается через собственные функции и собственные значения задачи Штурма-Лиувилля. Поэтому для таких задач метод функций Грина не имеет преимуществ по сравнению с методом разделения переменных. Его преимущество обнаруживается, если удаётся  сравнительно легко, не прибегая к разделению переменных, найти функцию Грина задачи. Такая ситуация характерна для задач о распространении тепла в безграничных или полуограниченных средах.

Прежде чем переходить к построению функции Грина, выясним её физический смысл. Рассмотрим решение одномерной, однородной задачи    

                             

Здесь  - начальное распределение температуры на отрезке . Пусть начальное распределение температуры создано только на отрезке.Тогда  

 

 есть количество теплоты, необходимое для создания начального распределения температуры,  при этом точка  принадлежит интервалу интегрирования. Устремляя  к нулю, получим

              

Из последнего соотношения следует физическая интерпретация функции Грина – она даёт пространственно-временное распределение температуры  при  , если в начальный момент  в точке  произошло повышение температуры на .

Аналогично можно интерпретировать решение неоднородного уравнения

                  

Здесь   задаёт мощность источников теплоты. Количество теплоты, выделившееся  за время от  до  на интервале , равно

                  

Пусть имело место только это тепловыделение. Тогда температура в точке x в момент времени  будет

      

                      

                     

                   ,      

Устремляя  и  к нулю, находим  . Функция Грина  даёт температуру в точке x в момент , если в точке  в момент  выделилось количество теплоты Q, повысившее температуру на . Ввиду такой интерпретации функцию Грина называют также функцией источника.

Перейдем к построению функции Грина уравнения теплопроводности.