4.1.5.2  ПОЛИНОМЫ ГИПЕРГЕОМЕТРИЧЕСКОГО ТИПА

 

Построить решение уравнения (4.281) можно, воспользовавшись тем фактом, что производная любого порядка от функции гипергеометрического (ГГ) типа  также есть функция ГГ типа. Чтобы показать это, продифференцируем уравнение (4.285).

                          

Для  получим уравнение

                          

или                                                        (4.289)

где                         ,      

Так как - полином степени не выше первой, то . Следовательно, (4.289) есть уравнение ГГ типа.  Справедливо и обратное: любое решение уравнения (4.289) при  есть производная от некоторого решения уравнения (4.285). Продифференцировав (4.289), получим

                                                      (4.290)

где                        

                         ,

                          

Выполним  то же для уравнения (4.290):

                                                       (4.291)

где                        

                         ,

                          

После  n - го дифференцирования будем иметь уравнение ГГ типа

                                                      (4.292)

где                        

                         ,

        

          

Таким образом, любое решение уравнения (4.291) можно представить в виде

                                

где  -  некоторое решение уравнения (4.285) . Это свойство позволяет построить семейство частных решений уравнения, соответствующих определенным значениям . При   (4.291) имеет решение . Тогда  из соотношения                              

                                  

повторным интегрированием получаем решение  уравнения (4.285) в виде  полинома  n - й  степени

                    

Такие решения называются полиномами  ГГ типа. Они соответствуют  собственным значениям

                                                              (4.293)

Явные выражения для полиномов  получим следующим образом. Умножим уравнения (4.285) и (4.292) на такие функции   и    соответственно, чтобы уравнения приобрели самосопряженный вид

                                                                          

                                                                

Сравнивая (4.293) с  (;.285) и (4.292), получим дифференциальные уравнения для  и

                                                                                           

                                                                                     

Из последних уравнений находим соотношения между    и :

        

          

          

,                                                (4.295)  

Так как  ,  ,   то из следует

                            

Откуда при   получаем

      

    

   

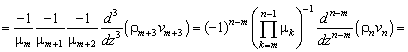
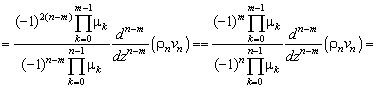
                                                                                (4.296)

где          ,            ,   .

Поскольку ,  а   ,  то   и  следует нумеровать еще и индексом n,  , .

Если   - полином  степени  n, то .  Тогда из (4.296) следует

               (4.297)

где  .  При  m = 0  получаем явные выражения для полиномов гипергеометрического типа

                 (4.298)

соответствующих   Соотношение (4.298) называется  формулой Родрига  (Б.О.Родриг, 1814г.). В ней  -  нормировочный множитель.