ДИФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ СПЕЦИАЛЬНЫХ ФУНКЦИЙ

 

Уравнения  (4.275), (4.277), (4.279)  можно представить в следующем общем виде

                                                 (4.281)

где -  полином не выше первой степени,  и  -  полиномы не выше второй степени. Например, для уравнения  (4.277) , . Переменная  z  может быть как вещественной, так и комплексной. Для уравнений типа (4.281), называемых  обобщенными уравнениями гипергеометрического типа,  развита общая теория, в изложении которой будем следовать книге  А.Ф.Никифорова и В.Б.Уварова [3].

Прежде всего, упростим уравнение (4.281) с помощью замены

                                 

где -  функция, которую предстоит определить. Подставив в  (4.281) производные

                          

получим уравнение

     (4.282)

Чтобы полученное уравнение  было не более сложным, чем (4.281), потребуем, чтобы коэффициент при   имел вид , где   -  произвольный полином степени не выше первой,

                                        

или                                                                              

Из уравнения (4.282) находим  . Выразим через  коэффициенты при  y  и :

          

    

        

        

        

          ;

          

Приходим к уравнению

                                                                (4.283)

- полином степени не выше второй, - полином степени не выше первой, поэтому уравнение (4.283) принадлежит к тому же типу, что и (4.281). Подберём коэффициенты полинома так, чтобы полином  делился без остатка на полином , то есть  чтобы

                                         ,

 или  ,  (4.284)

где  . Уравнение (4.283) примет вид

                                                             (4.285)

Оно называется  уравнением гипергеометрического типа, а его решения - функциями гипергеометрического типа. Так как , то (4.284) есть квадратное уравнение относительно ,

                    

из которого находим

 

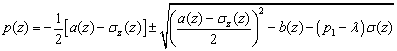
(4.286)

Чтобы  был полиномом первой степени, под корнем должен стоять квадрат полинома первой степени. Произвольный полином второй степени  можно представить в виде

      

                    ,

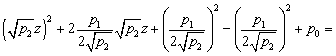
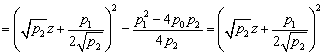 при условии                                                  (4.287)

Если обозначить                                                   (4.288)

то  (4.287) есть уравнение для определения k. Коэффициенты  выражаются через коэффициенты полиномов , поэтому они содержат параметры исходной задачи, в частности, безразмерную энергию  и  квантовое число l. Таким образом, приведение уравнения (4.281) к форме уравнения гипергеометрического типа возможно только при некоторых значениях параметра  k, а, значит, и энергии  E. После определения k находим   и  выражаем  решение уравнения (4.281) через функции гипергеометрического типа.