ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ

 

Решения уравнения Лапласа  называются гармоническими функциями. Легко могут быть найдены гармонические функции, обладающие сферической или цилиндрической симметрией. В первом случае уравнение Лапласа принимает вид

                              

откуда находим         ,    

Если наложить условие , то . В этом случае  решение

                                                                         (4.238)

можно отождествить с потенциалом точечного заряда в пустом пространстве. Во втором случае имеем уравнение

                              

Его решение  можно отождествить с потенциалом положительно заряженной линии, если положить . Тогда

                                                                 (4.239)

  и    называются фундаментальными решениями уравнения Лапласа в пространстве и на плоскости соответственно, за исключением точки в начале координат .

С помощью формул Грина, известных из математического анализа, можно установить ряд общих свойств гармонических функций.

Согласно теореме Грина, если внутри области D, ограниченной поверхностью S, заданы функции  и , непрерывные вместе с производными до второго порядка включительно везде в D вплоть до поверхности, то справедливо интегральное равенство

               (4.240)

Здесь  - производная по внешней нормали к S (рис. 4.19).

                 

 

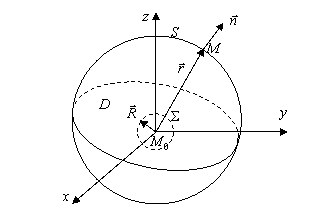
            Рис. 4.19  К  выводу свойств гармонических функций

Положим ,  - расстояние от фиксированной точки  до произвольной точки . Область  получена исключением из D шара радиусом R с центром в точке . Всюду в   ограничена и  , поэтому

      

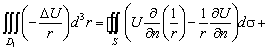
                                                 (4.241)           

  - поверхность шара Q. Так как на ней , то  вместо (4.241) получим

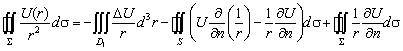
Интегралы по поверхности    оценим с учётом того, что :

      

      

Устремим радиус шара к нулю. Если нормальная производная ограничена на его поверхности, то второй интеграл исчезает, а первый превращается в . Если к тому же функция U удовлетворяет уравнению Лапласа, то её значение в точке  выразится через значения на поверхности S,

                                (4.242)

Рассуждая аналогично, для решения двумерного уравнения Лапласа можно получить формулу

                          (4.243)

где L – контур, ограничивающий двумерную область D. Из формул (4.242) и (4.243) следуют свойства гармонических функций.

1. Если взять ,  , то

                                             (4.244)

Свойство (4.244) означает, что поток вектора градиента гармонической функции  через замкнутую поверхность S равен нулю – сколько  втекает в D, столько же и вытекает. Это эквивалентно отсутствию в D источников функции U. При наличии источников невозможно стационарное состояние. Это особенно наглядно, если U –температура. Внутренние источники при отсутствии оттока тепла через границу  непрерывно разогревали бы объем D.

2. Если S – сфера радиуса R, то   и

                                   (4.245)

Значение гармонической функции в центре сферы можно найти через её значения на поверхности сферы.

3. Если проинтегрировать по поверхности S граничное условие Неймана, то получим

                                                (4.246)

Неоднородность в граничном условии должна содержать как положительные, так и отрицательные источники (стоки), компенсирующие действие друг друга.