ОСТЫВАНИЕ ШАРА

 

Рассмотрим задачу об остывании однородно нагретого шара, аналогичную п.1.4.2.6. Она дает возможность изучить решения уравнения теплопроводности в сферической системе координат. При этом мы придем к необходимости изучить свойства новых собственных функций и собственных значений  задачи Штурма-Лиувилля.

Физическая постановка задачи такова: найти температуру внутри шара радиуса  R  при  , если при    он погружается в среду с температурой   и  бесконечной теплоемкостью. Начальная температура шара , все теплофизические параметры постоянны.

Нетрудно сформулировать ее математически: найти решения уравнения

                                            

удовлетворяющее начальному                   

и граничному                                    

условиям.

Как и в задаче об остывании цилиндра, введём безразмерные переменные

   

Вместо (4.155) получим

                                                

                                                         

                                                                  

Решение задачи (4.156) ищем методом разделения переменных. В соответствии с общей теорией оно имеет вид

                           (4.157)  есть решение задачи Штурма - Лиувилля

                                                                      

                                                                     

В сферической системе координат уравнение (4.158') имеет вид   

   

                                                                                          (4.159)

Будем искать его решение в виде

                                                   (4.160)

Подставляем (4.160) в (4.159):

      Делим на  RY  и  умножаем  на  :

Разделяем пространственные и угловые переменные:

     

                                             

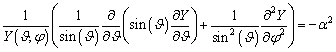
Рассмотрим подробно  уравнение

      

Решения его называются сферическими функциями. Для их  нахождения произведем дальнейшее разделение переменных

                                                         (4.162)

После подстановки в  имеем

        

Разделяя полярный и азимутальный углы, получим уравнение для 

                                

имеющее решения      

или                                                             (4.163)

Из условия однозначности азимутальной функции 

 

следует, что .Азимутальные функции   с целыми индексами обладают свойством ортогональности

                                              (4.164)

Звёздочка означает комплексное сопряжение. Функция  удовлетворяет, таким образом, уравнению

                  

или 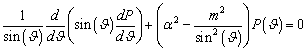                         (4.165)

Преобразуем его с помощью замены переменных  . Так как , то  . Получаем уравнение

                                (4.166)

Оно имеет стандартный вид уравнения Штурма - Лиувилля. Точки   являются его регулярными особыми точками. В них коэффициент при  P  обращается в бесконечность.

Решения уравнения (4.166) называются присоединенными полиномами Лежандра. Их явный вид можно было бы найти методом Фробениуса. Для этого P(y) следует искать в виде

                                

Функция   должна удовлетворять уравнению

 ,

которое не содержит сингулярности при  . Если   представить в виде ряда

                               ,

то для его коэффициентов можно получить соотношения

                              

                              

                    

Чтобы ряд был ограниченным в точках  , он должен содержать конечное число членов, то есть быть полиномом. Если  положить, ,  но , то получим собственные значения

                              

Так как    то и , при этом ,  .

Таким образом, приходим к выводу, что присоединенные полиномы Лежандра  зависят от двух индексов, n  и  m. Их принято обозначать . Все их свойства можно было бы вывести из соотношений между коэффициентами. Однако усилиями великих математиков позапрошлого века разработан гораздо более  изящный и  удобный метод изучения  свойств решений уравнения (4.166) с помощью производящей функции, которым мы и воспользуемся.