СФЕРИЧЕСКИЕ ФУНКЦИИ БЕСЕЛЯ

 

Возвратимся к уравнению . С учётом найденного собственного значения  оно принимает вид

                                       (4.197)

Перейдем к переменной ,

                                        

а затем сделаем подстановку  .

                  

                  

      

                         

      

                  

или 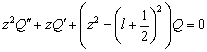                                    (4.198)

Получили уравнение Бесселя для функции полуцелого индекса. Его общее решение есть линейная комбинация соответствующих функций Бесселя и Неймана

            

Радиальная же функция

                     

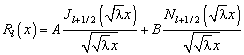
будет линейной комбинацией сферических функций Бесселя и Неймана, определяемых соотношениями

                 

Свойства сферических функций Бесселя и Неймана следуют из ранее установленных свойств функций Бесселя и Неймана. В частности,  - ограничена, а - расходится при . Поэтому в   (4.199) полагаем . Соотношения ортогональности для можно получить из (4.197).

Запишем это уравнение для функций   и  :

               (Д1)

              (Д2)

Умножим первое из них на    и вычтем из него второе, умноженное на   :

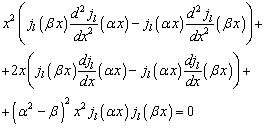                                (Д3)

Первые два слагаемых можно представить в виде производной,

          

                       

                                  

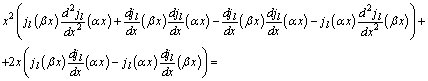
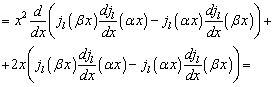
Проинтегрируем (Д4) по x от 0 до 1,

               

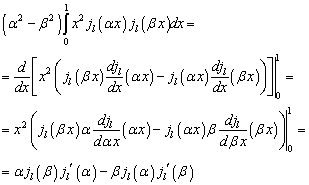
Если     (корни уравнения  или   - разные), то правая часть) равна нулю и , следовательно ,

                                                                      (Д5)

При   из (Д5) находим квадрат нормы функции  ,

                        

 

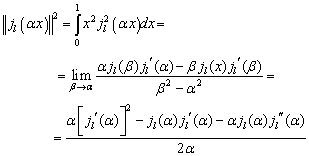
Подставив вторую производную из  

                   ,

получим

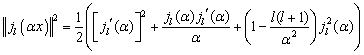  (Д7)

Таким образом, условие ортонормировки запишем в виде

                                   (4.201)

Из соотношений (4.130) следуют рекуррентные соотношения для сферических функций Бесселя

                                                    (Д8)

                                                            (Д9)

Из симметрии задачи следует, что поле температур внутри шара не зависит от  и . Это возможно, если . Поэтому

                  

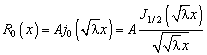
Собственные значения   находим из условия

                  

Следовательно, корни функций  и  совпадают. Обозначая их через , запишем общее решение задачи о поле температур внутри шара в виде

                                      (4.202)

Коэффициенты  найдем с помощью соотношений (4.201), (Д7), (Д8)

                  

 

    

 

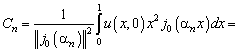
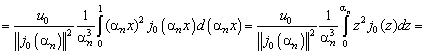
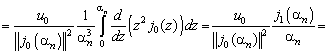
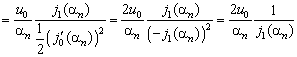
Таким образом, безразмерное поле температур внутри шара даётся выражением

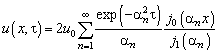                                   (4.203)

В размерных величинах оно имеет вид     

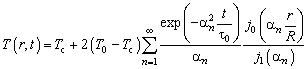            (4.204)