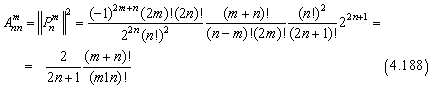ПРИСОЕДИНЁННЫЕ ПОЛИНОМЫ ЛЕЖАНДРА                                           

Продифференцируем  уравнение Лежандра

                    

m раз по формуле Лейбница

              

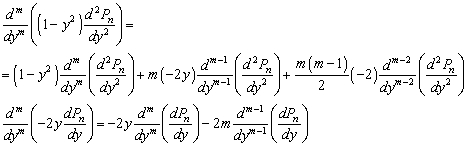Обозначим  . Для  u  получим уравнение

   

или     

Образуем функцию   и выразим через нее производные функции :

 

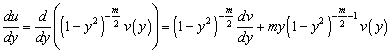
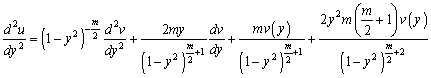 Подставим  производные в уравнение для u. После сокращения на  и приведения подобных членов получим уравнение для  :

              

Функция    удовлетворяет уравнению для присоединенных полиномов Лежандра. Следовательно,

                                         (4.183)

В формуле (4.183) должно быть , так как операция дифференцирования с   не определена. Если подставить в (4.183) формулу Родрига,

                      

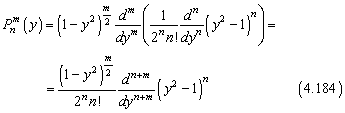
то такое определение полиномов Лежандра можно распространить и на случай  , так как . Из (4.183) сразу следует

                                

а из (4.184) легко найти несколько первых присоединенных полиномов Лежандра:

        

        

        

        

        

        

                    

      

               

                

Графики нескольких присоединенных полиномов Лежандра в полярной системе координат показаны на рис.4.15

                     

 

      Рис.4.15  Графики полиномов                                                                                                     

4.1.2.8.3. СВОЙСТВА ПРИСОЕДИНЁННЫХ ПОЛИНОМОВ ЛЕЖАНДРА

 

1. Четность. Из определения присоединенных полиномов Лежандра (4.185) следует

                                                   (4.186)

 

2. Ортогональность. Присоединенные полиномы Лежандра ортогональны на промежутке  с весом  ,

                               (4.187)

Доказательство: вычислим интеграл ортогональности с использованием определения присоединенных полиномов Лежандра

    

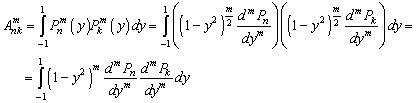
После  m -кратного интегрирования по частям получим                   

          

Используем формулу Родрига и интегрируем по частям еще  k - раз:

 

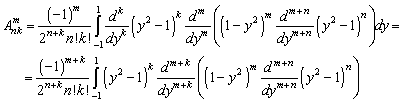
Применим формулу Лейбница  для дифференцирования под интегралом

 

Производные не равны нулю, если

                              или       

         и                   или      

Сложив два неравенства, получим .  Но это неравенство невозможно при , так как . Поэтому все производные равны нулю и, следовательно,  при  . Только при   возможно равенство  . В сумме при этом останется одно слагаемое с   :

  Производные под интегралом равны

         ,              

Следовательно,

          

Интеграл преобразуем к тригонометрической форме

                          

Последний интеграл сводится к  - функции. По определению,

          

При  n = m

  Таким  образом,