СТАЦИОНАРНАЯ ДИФФУЗИЯ НОСИТЕЛЕЙ ЗАРЯДА В ЦИЛИНДРИЧЕСКОМ p-n -ПЕРЕХОДЕ

 

В п.1.2 получено уравнение, описывающее диффузию рекомбинирующих носителей заряда,

                                 

В векторном инвариантном виде оно справедливо в любой системе координат.

Рассмотрим инжекцию через цилиндрический  p-n - переход. Будем представлять его в виде бесконечной  цилиндрической  - области  в безграничной среде с проводимостью  n - типа. Вокруг - цилиндра образуется  цилиндрическая область пространственного заряда радиусом . Если к   - области приложить прямое смещение, то дырки будут инжектироваться через  p-n - переход  и диффундировать в n - области. Стационарное распределение их описывается уравнением

                                                           (4.141)

или                                                           

где  ,  - равновесная концентрация дырок в n – области. Найдем это распределение  при следующих краевых условиях:

1. на большом по сравнению с диффузионной длиной расстоянии от границы области пространственного заряда (ОПЗ) концентрация дырок равна равновесной, а, следовательно, их избыточная концентрация равна нулю,

                      или                   (4.142)

2. на границе ОПЗ при  задана плотность тока инжекции ,

                                                          (4.143)

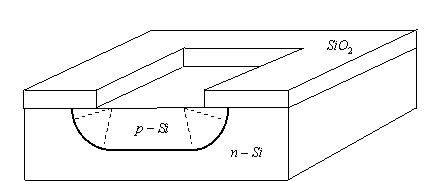
Модель может показаться до некоторой степени искусственной, однако она может аппроксимировать реальную ситуацию в планарных приборах. Профиль p - кармана, образованного диффузией примеси через узкое окно, показан на рис.4.12.

    

 

                 Рис.4.12 Профиль планарного  p-n – перехода

 

В секторах, ограниченных пунктирами, профиль приближенно цилиндрический. В этих секторах распределение концентрации неосновных носителей заряда описывается  решением уравнения (4.141) с граничными условиями (4.142), (4.143).

Запишем (4.141) в цилиндрической системе координат

                                     (4.144)

Решение ищем  методом разделения переменных:

                                

        

         

                              

                

Радиальная функция удовлетворяет уравнению

                                     (4.145)

которое после перехода к  безразмерной переменной  примет вид                                         

С помощью замены     приводится к уравнению  Бесселя

                    

 

Следовательно, решением   являются   функции Бесселя от мнимого аргумента .  Из определения функций Бесселя  находим:

            

                        

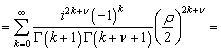
                       (4.146)

Вещественный ряд  также является решением  уравнения . Его принято называть  модифицированной функцией Бесселя первого рода  или  функцией Бесселя мнимого аргумента первого рода

                                                            

Свойства  следуют из ранее установленных свойств .Из находим первое рекуррентное соотношение

       

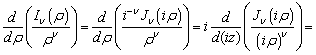
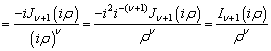                                 (4.147)

Второе  рекуррентное соотношение получим из  :

         

          

С другой стороны,

           

Сравнивая правые части двух последних равенств, находим                 

                                                (4.148)

Выполняя непосредственное дифференцирование в (4.147) и (4.148), получаем         

  или                                                            

                                                                         

Из  ) и   следует

                                                            (4.150)

При нецелых  ν  функции   и    линейно независимы.  Через них определяется второе решение уравнения (4.145'), называемое модифицированной функцией Бесселя второго рода, или функцией Бесселя мнимого аргумента второго рода, или функцией Макдональда ,

                                                (4.151)

При целых     ,  поэтому  определяется аналогично функции Неймана     

                                          (4.152)

Графики функций   и    показаны на рис.4.13.

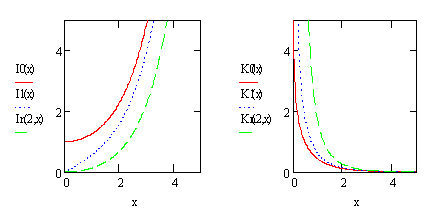
       Рис.4.13   Графики  функций  Бесселя мнимого аргумента

 

Модифицированные функции Бесселя первого и второго рода являются монотонными. Асимптотически они ведут себя следующим образом:

       при              ,

                                         ,

       при                ,

                                          .

Общее решение уравнения  представляется в виде

                        

Из условия ограниченности решения на бесконечности следует . Концентрация диффундирующих носителей не должна зависеть от азимутального угла , поэтому полагаем  . Таким образом,

                                

или в размерных переменных

                                                      (4.153)

постоянную  А  находим из граничного условия  (4.143):

                               ,

или                  

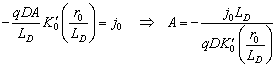
Так как ,  то окончательно получаем

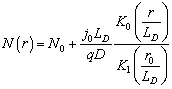                                               (4.154)