4.1.2.4   ЗАДАЧИ О РАСПРОСТРАНЕНИИ ГРАНИЧНОГО РЕЖИМА

                 

Изложенный в предыдущем пункте метод решения краевых задач можно обобщить на случай  нестационарных  граничных условий. Например, на одной из граней пластины может быть задан закон изменения температуры со временем

                                

Такие задачи решаются по следующей схеме, называемой методом   Дюамеля.

1. Сначала решаем задачу со стационарной неоднородностью , соответствующую некоторому фиксированному моменту времени   ,

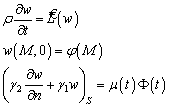                                                (4.85)

Неоднородность включается в момент  t = 0, и при имеет постоянное значение, соответствует  моменту    (рис. 4.5)

   

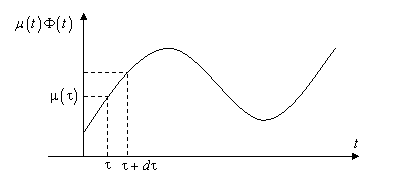
             Рис.4.5  Временная зависимость граничных условий

 

Обозначим это решение через . Согласно п.4.1.2.3,

                                                  (4.86)

где  - решение задачи .

2. Решением задачи (4.85) с краевыми условиями, включенными в момент  ,

                          

будет функция  (4.86) со сдвинутым временным аргументом .

3. Решением задачи (4.84) с краевыми условиями, включающимися в момент    и  выключающимися в момент                      

      

 будет функция

                                          (4.87)

4. Наконец, если, начиная с момента  t = 0, действуют краевые условия общего вида

                              

то решение задачи  будет суммой (интегральной) решений (4.87),

                        (4.88)

Выполним дифференцирование под знаком интеграла в (4.88) с учетом  свойства ступенчатой функции Хэвисайда

                                

где   -  δ - функция Дирака.  Получим  

      

                  

                               (4.89)

Таким образом, решение задачи о распространении произвольного граничного режима  легко находится, если известно решение задачи (4.85) с единичной неоднородностью в граничных условиях.