ЗАДАЧИ С НЕОДНОРОДНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ    

       

Решение задачи п.4.1.2.2 получено сравнительно легко из-за однородности краевых условий первого рода.

Рассмотрим теперь случай, когда на одной из боковых граней пластины поддерживается  при  t > 0  температура , отличная от начальной температуры . Поле температур в пластине в этом случае является решением задачи

                    

                                                                        (4.72)       

                               ,           

                    

Применяя процедуру предыдущего пункта, перейдем к безразмерным переменным X, Y,  и приращению температуры :

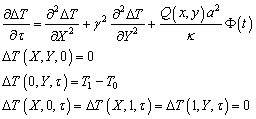                           (4.73)

Произведем редукцию задачи (4.73), то есть будем искать её решение в виде

                    

Функция  есть решение краевой задачи

                  

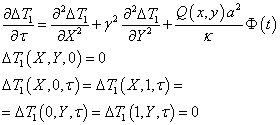
Решение её было получено ранее (формула (4.70)). Функцию  найдем из краевой задачи

                          

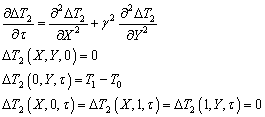
Задачу  можно еще упростить, введя безразмерную температуру : 

               

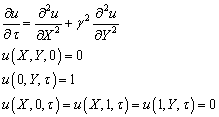
 Решение её будем искать в виде

                                       (4.75)

где  -  решение стационарной задачи

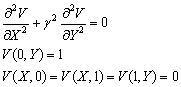                                            (4.76)

a   -  отклонение  от  стационарного решения. Для него задача ставится следующим образом:                

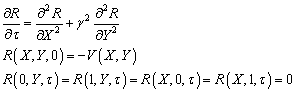               (4.77) 

Задачу (4.76) решаем методом разделения переменных. Представляем решение в виде    , подставляем его в (4.76)      

                             ,

делим на :        

и разделяем переменные

                  ,    

или                                 ,                                                                                                               

Из граничных условий  (4.76)   следуют  граничные условия для 

                            ,                          

Уравнению  и первому условию (4.77''') удовлетворяет функция   . Из второго условия  находим 

          ,      

Общие  решения уравнений (4.77')  и  (4.76) запишем в виде

        

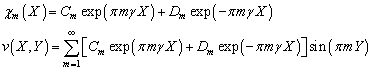
 Постоянныеинайдем из второй пары краевых условий (4.76):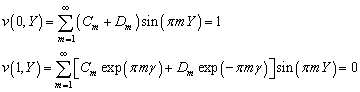              

Из второго из них  ввиду линейной независимости функций    следует

                                   

Первое уравнение умножаем на  и интегрируем по Y c учётом соотношения ортогональности  функций  и  : 

                          

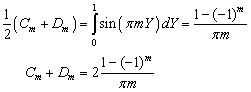
Умножая  поочередно на  и   и, вычитая его после этого из , найдем

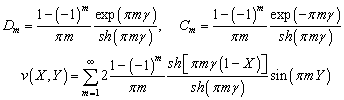      (4.79)

Решение задачи (4.77) дается формулами (4.15) и (4.17):

          (4.80)

                  (4.81)

Явное выражение для  коэффициентов получим, подставив (4.79) и (4.81) и выполнив интегрирование:

         

   

   

                                                      

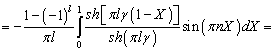
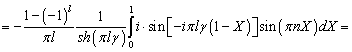
Таким образом,

                                                                                         (4.82)

Собственные значения даются формулой (4.64). Тем самым завершено построение решения краевой задачи с неоднородным постоянным краевым условием первого рода:

                   (4.83)

                          (4.84)

Графики функций   представлены на рис.4.5

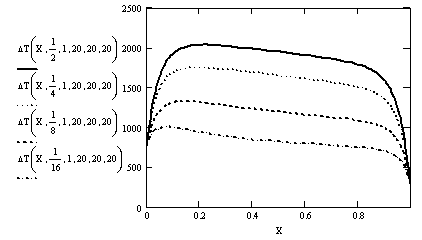
   Рис. 4.5а  Распределение температуры  в различных Y - сечениях

                    пластины

 

 

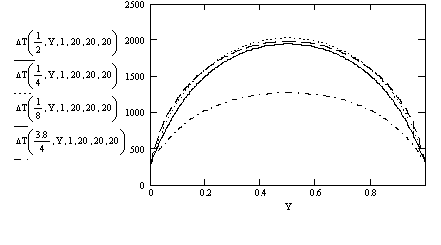        Рис. 4.5б  Распределение температуры  в различных X - сечениях

                     пластины