ДВУМЕРНАЯ ТЕПЛОПРОВОДНОСТЬ В ПЛАСТИНЕ

 

Рассмотрим обобщение предыдущей задачи: найти распределение температуры в пластине  c  теплоизолированными  основаниями  и , если   при   боковые грани её поддерживаются при температуре , а в объеме действуют тепловые источники  мощностью . Начальная температура  - , все теплофизические параметры пластины постоянны (рис.4.3)

 

             .    

       Рис.4.3              Геометрия задачи о двумерной теплопроводности

 

Так как основания пластины теплоизолированы, то тепло распространяется в плоскости пластины x,y. Искомое поле температур   есть решение задачи

                                     (4.50)

                                                                     (4.51)

                               (4.52)

Аналогично задаче п.4.1.2.1  переходим к безразмерным переменным

                       

и приращению температуры . Для  получаем задачу

                             

                                                                  

         

Общее решение ее запишем согласно теории метода разделения переменных,

                                      

Собственные функции  и собственные значения  находим из задачи Штурма – Лиувилля

                                                                      (4.53)

                                                          (4.54)

                                                           (4.55)

Оператор Штурма - Лиувилля   есть сумма двух операторов, действующих на разные переменные. Поэтому собственную функцию целесообразно искать в виде произведения функций от одной переменной

                                

Уравнение (4.53) примет вид

                                

Разделим его на  :

                              

Сумма двух функций от разных  переменных  равна постоянной величине, только если каждая из них равна некоторой постоянной:

                                                                     (4.56)

                                                                 (4.57)

                                                                           (4.58)

Из (4.54) и (4.55) следуют граничные условия для  и :

                                                                 (4.59)

                                                                 (4.60)

Решения уравнений (4.56), (4.57), удовлетворяющие условиям (4.59), (4.60), легко находятся:

                  (4.61)

            (4.62)

Таким образом, собственные функции и собственные значения задачи Штурма - Лиувилля

                                              (4.63)

                                           (4.64)

нумеруются двумя индексами. Поэтому общее решение запишем в виде двойной суммы

    (4.65)

Уравнение для функций    находим, подставив (4.65) в :

,

                  

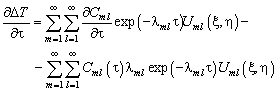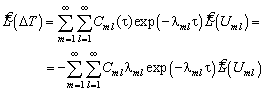
                   (4.66)

Воспользуемся ортогональностью функций .  Умножим (4.66) на  и проинтегрируем по площади пластины:

      

                                         (4.67)

Двойной интеграл слева распадается на произведение двух однотипных интегралов по  и по .

  

           

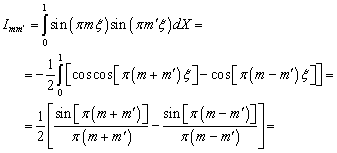
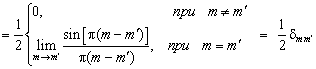
Аналогично                     

Интеграл справа в (4.67) также распадается на произведение двух   интегралов, типа вычисленного в п.4.1.2.1:

                    

Вместо (4.67)  теперь имеем

     

 

Откуда находим :

        

  

Так как   при четных  m', l'  , то только коэффициенты   с нечетными индексами , ,  ,  не равны нулю:

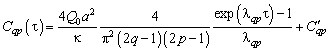                   (4.69)

  при нулевых начальных условиях. После этого получаем окончательное выражение для поля температур в безразмерных переменных

 

                                          

 

         

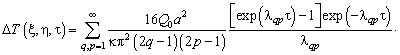
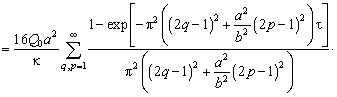
                                     (4.70)

(4.70) обнаруживает большое сходство с распределением температуры в стержне. Поэтому сохраняют силу качественные оценки п.4.1.2.1.  Пространственно-временнόе поведение поля температур описывается функцией

  

где 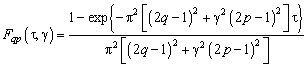            (4.71)

Eё  сечения плоскостями   и  показаны на рис.4.3а, б.

 

 

 

  

    Рис.4.3а Распределение температуры по срединным сечениям

                    пластины  при  и  различных значениях .

 

 

 

    

 

       

 

    Рис.4.3б Распределение температуры по различным  продольным

                   и поперечным  сечениям пластины при .

 

Из графиков видно, что решение (4.70) качественно ведет себя вполне "физически разумно". Для полной убежденности в правильности желательно проверить его количественно. Вычислим с этой целью полный поток теплоты, вытекающий из пластины вовне через четыре боковые грани. В стационарном состоянии, достигаемом при , этот поток должен равняться полной мощности источников теплоты в пластине.

Плотность теплового потока в точке (x,y) в момент времени t равна

       

Поток через грань (x=a,y)

        

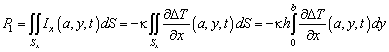
Здесь  h - толщина пластины. Перейдем к безразмерным переменным:

        

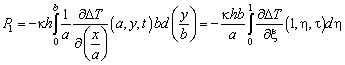
В силу симметрии задачи такой же поток тепла вытекает через грань 3,  . Аналогично запишем равные потоки через грани 2 и 4

                    

Суммарный поток  равен

    

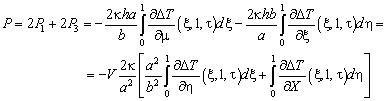
где  - объем пластины.  Из (4.70) находим производные:   

          

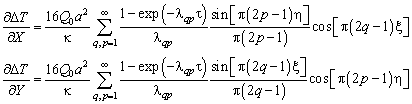
Так как

,  

то при            

                    

                  

      

 

                  

 

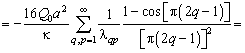
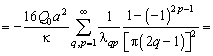
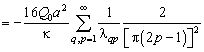
Аналогично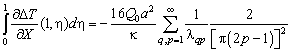   

Теперь полный поток находится  тривиально:

      

      

      

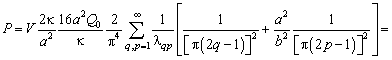
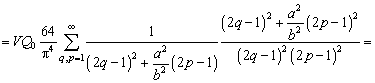
Суммы по p и по q  одинаковы и равны  каждая   [9].   Поэтому                                                        

Таким образом, из каждой единицы объема пластины во внешнюю среду уходит  теплоты. Следовательно, решение (4.70) правильное.